1517. Простое сложение
Определим следующую
рекурсивную функцию F(n):
F(n) = 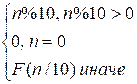
Определим функцию S(p, q)
следующим образом:
По заданным p и q вычислите S(p, q).
Вход. Состоит из нескольких тестов. Каждая строка содержит два
неотрицательных целых числа p и q (p
≤ q), разделенных пробелом. p и q
являются 32 битовыми знаковыми целыми. Последняя строка содержит два
отрицательных целых числа и не обрабатывается.
Выход. Для каждой пары
p и q
в отдельной строке выведите значение S(p, q).
|
Пример
входа |
Пример
выхода |
|
1 10 10 20 30 40 -1 -1 |
46 48 52 |
РЕШЕНИЕ
рекурсия
Анализ алгоритма
Приведенная в
условии функция f(n) находит последнюю ненулевую цифру числа n.
Например, f(1234) = 4, f(3900) = f(390)
= f(39) = 9.
Обозначим через
Тогда S(p, q) = g(q) – q(p – 1).
Для вычисления функции g(p),
суммы последних значащих цифр для чисел от 1 до p, разобьем числа от 1 до p
на три множества (операция деления ‘/’ является целочисленной):
1. Числа от (p / 10) *
10 + 1 до p;
2. Числа от 1 до (p / 10)
* 10, не оканчивающиеся нулем;
3. Числа от 1 до (p / 10)
* 10, оканчивающиеся нулем;
Сумма последних значащих цифр в первом множестве
равна 1 + 2 + … + p mod 10 = t * (t
+ 1) / 2, где t = p mod 10. Во втором множестве искомая
сумма равна p / 10 * 45, так как
сумма всех цифр от 1 до 9 равна 45, а число полных десятков равно p / 10. Требуемую сумму для третьего
множества найдем рекурсивно: она равна g(p
/ 10). Получим рекуррентность:
g(p) = ![]() +
+  +
+  , t = p mod 10
, t = p mod 10
g(0) = 0
Пример
При p = 32 к первому множеству отнесутся
числа 31, 32, ко второму 1, …, 9, 11, …,
19, 21, …, 29, к третьему 10, 20, 30. Значение t = 32 mod 10 = 2.
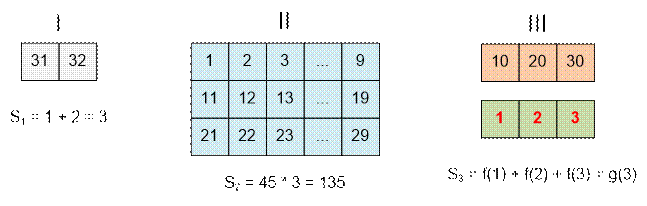
g(32) = ![]() + 45 * 5 + g(3) = 3 + 135 + (1 + 2 + 3) = 144
+ 45 * 5 + g(3) = 3 + 135 + (1 + 2 + 3) = 144
Пусть p = 1234.

g(1234) = ![]() + 45 * 123 + g(123) = 10 + 5535 + g(123) = 5545 + g(123)
+ 45 * 123 + g(123) = 10 + 5535 + g(123) = 5545 + g(123)
Вычислив значение
g(123) = 595, получим:
g(1234) = 5545
+ g(123) = 5545
+ 595 = 6140
Реализация алгоритма
Поскольку
выполняется обработка 32-битовых знаковых чисел, то для избежания переполнения при
вычислениях используем тип long long.
long long p, q;
Функция g вычисляет сумму значений функции f(n) для значений
аргумента n от 1 до p.
long long
g(long long p)
{
long long t = p % 10;
if (p <= 0) return
0;
return t * (1
+ t) / 2 + p / 10 * 45 + g(p / 10);
}
Значение функции
S(p,
q) считаем как g(q)
– q(p – 1).
long long
s(long long p, long long q)
{
return g(q) -
g(p - 1);
}
Основной цикл
программы. Для каждой пары чисел p и q выводим значение s(p, q).
while(scanf("%lld
%lld",&p,&q), p + q >= 0)
printf("%lld\n",s(p,q));
Java реализация
import java.util.*;
public class Main
{
static long g(long p)
{
long t = p %
10;
if (p <=
0) return 0;
return t * (1
+ t) / 2 + p / 10 * 45 + g(p /
10);
}
static long s(long p, long q)
{
return g(q) - g(p -
1);
}
public static void
main(String []args)
{
Scanner con = new
Scanner(System.in);
while(true)
{
long p = con.nextLong();
long q = con.nextLong();
if ((p <
0) && (q < 0)) break;
System.out.println(s(p,q));
}
con.close();
}
}
Python реализация
Функция g вычисляет сумму значений функции f(i) для значений
аргумента i от 1 до n.
def g(n):
if n <= 0: return 0
t = n % 10
return (n // 10) * 45 + (t * (t + 1) // 2) + g(n
// 10)
Основной цикл
программы.
while
True:
p, q = map(int, input().split())
if p < 0 and q < 0: break
Для каждой пары
чисел p и q выводим значение s(p, q) = g(q) – g(p
– 1).
print(g(q) - g(p - 1))

